
In my previous post we implemented and tested several basic reinforcement learning agents. In this post we take a short break from deep learning and explore the FFAI Blood Bowl gym environment. We examine the state space and action space. We will also manually run through a couple actions exploring the changing state as we go. All of the code I used to generate the plots in this post is available in this Jupyter notebook.
The FFAI Blood Bowl environment state consists of three components: the board, game state, and game procedure. The board is a tensor with features and a board size of . Below is a plot of each feature after running a game a little bit past the setup phase.

Some of these data are binary; such as which spaces are occupied, the location of your endzone, which players have a certain skill (block, dodge), which player is currently active, and the available positions that active player can move to. Other data is scaled between zero and one; the values of the various player attributes, the number of players contributing to a given tackle zone, and the dodge roll probabilities.
For example, below is a plot of our own players in dark red, the opposing players in orange, and the roll probabilities of the active player in blue.
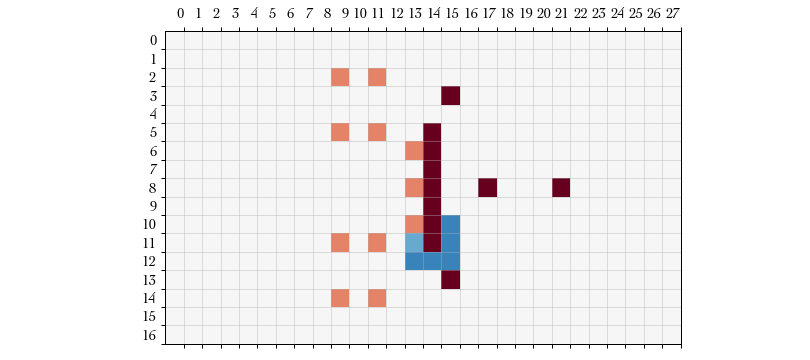
We see that this is consistent with the movement rules from the Blood Bowl Living Rule Book v6.0 where the probability of success is inversely proportional to the number of opposing tackle zones on the square that the player is dodging into.
While the board state contains various geometric data, the game state is a
vector containing non-geometric, higher-level, normalized
information about the game. For example, the features half and round tell us
when we are in the current game, own score and opp score store the numbers
of touchdowns scored by each team, and is blitz available and is blitz lets
us know the the blitz action can be taken and is currently being used,
respectively. Finally, the game procedure is a one-hot vector
encoding which part of the game we are currently in. Every new game begins in
the StartGame procedure, represented by the vector . It then transitions into the CoinTossFlip,
CoinTossKickReceive, Setup, and PlaceBall, procedures before finally
entering the Turn procedure during which the bulk of the game takes place.
During the turn, however, there are multiple occurrences of the PlayerAction,
Block, Push, and FollowUp, procedures where the players needs to make a
decision about who to block, if successful choosing which square to push the
opponent into, and whether or not to follow up. In other words, these procedures
encode when only certain subsets of actions are allowed at a given time.
Given the state of the board above it turns out that we are in the
PlayerAction procedure, meaning that the currently active player has a variety
of actions available to them like moving and blocking. The game state is,
>>> observation['state']
{'half': 0.0,
'round': 0.125,
'is sweltering heat': 0.0,
'is very sunny': 0.0,
'is nice': 0.0,
'is pouring rain': 0.0,
'is blizzard': 0.0,
'is own turn': 1.0,
'is kicking first half': 1.0,
'is kicking this drive': 1.0,
'own reserves': 0.0625,
'own kods': 0.0,
'own casualites': 0.0,
'opp reserves': 0.0625,
'opp kods': 0.0,
'opp casualties': 0.0,
'own score': 0.0,
'own turns': 0.125,
'own starting rerolls': 0.375,
'own rerolls left': 0.5,
'own ass coaches': 0.125,
'own cheerleaders': 0.25,
'own bribes': 0.0,
'own babes': 0.0,
'own apothecary available': 0.0,
'own reroll available': 1.0,
'own fame': 1,
'opp score': 0.0,
'opp turns': 0.125,
'opp starting rerolls': 0.375,
'opp rerolls left': 0.375,
'opp ass coaches': 0.125,
'opp cheerleaders': 0.25,
'opp bribes': 0.0,
'opp babes': 0.0,
'opp apothecary available': 0.0,
'opp reroll available': 1.0,
'opp fame': 0,
'is blitz available': 1.0,
'is pass available': 0.0,
'is handoff available': 0.0,
'is foul available': 1.0,
'is blitz': 0.0,
'is quick snap': 0.0,
'is move action': 0.0,
'is block action': 0.0,
'is blitz action': 0.0,
'is pass action': 0.0,
'is handoff action': 1.0,
'is foul action': 0.0}
As mentioned, the game has only been simulated a little bit past setup so we
are still in the first half (half == 0.0) and the second round (round ==
0.125). The current game has normal weather effects and it is currently our
turn, which we already knew based on the current roll probabilities. We elected
to kick during setup and the current drive is a result of the kickoff
reception, as opposed to inducing a fumble from an opponent’s drive.
Actions in FFAI are encoded action type and position tuples, . The
action type is one of thirty-seven possible actions, such as START_GAME,
USE_REROLL, SELECT_PLAYER, MOVE, and BLOCK. Of these thirty-seven
actions, twenty-two of them use the positional input . For example, the
coordinates of SELECT_PLAYER indicate which player is selected for the next
action. Then, once that player is selected they can MOVE to potentially one of
eight adjacent locations on the board as long as they are unoccupied. The input
coordinates indicate which location the player moves into. Positional input is
ignored by the other actions, like START_GAME and USE_REROLL.
To get a better idea of how the board, state, and procedure interact with the actions we randomly set up a game and then manually step through several actions. Each step below shows a list of currently available actions we can take, the current procedure, and a plot of the board. The board plot shows our opponent’s players in orange, our own players in red, and the current roll probabilities in blue if available. You can generate these plots for yourself by running through this notebook.
Action #1: START_MOVE – Immediately after setup we lave a long list of
available actions. Below we only show the first two action types and available
positions but other available action types include START_BLITZ, START_PASS,
START_HANDOFF (turns out there was a touchback during kickoff so one of our
players begins with the ball!), and START_FOUL.
ActionType.START_MOVE (id = 27)
{'x': 15, 'y': 3}
{'x': 14, 'y': 5}
{'x': 14, 'y': 6}
{'x': 14, 'y': 7}
{'x': 14, 'y': 8}
{'x': 17, 'y': 8}
{'x': 21, 'y': 8}
{'x': 14, 'y': 9}
{'x': 14, 'y': 10}
{'x': 14, 'y': 11}
{'x': 15, 'y': 13}
ActionType.START_BLOCK (id = 28)
{'x': 14, 'y': 5}
{'x': 14, 'y': 6}
{'x': 14, 'y': 7}
{'x': 14, 'y': 8}
{'x': 14, 'y': 9}
{'x': 14, 'y': 10}
{'x': 14, 'y': 11}
... (snip) ...
ActionType.END_TURN (id = 8)
Current procedure: Turn (index = 7)

The action types we will explore throughout this example are START_MOVE and
START_BLOCK. For START_MOVE, the available positions correspond to our
players who are eligible to move. Here we select START_MOVE = 27 for the
player at . Below we specify the action tuple and step the
environment.
action = {
'action-type': 27, # START_MOVE
'x': 14,
'y': 11,
}
observation, reward, is_terminal, _ = environment.step(action)
Action #2: MOVE – The game procedure switches to PlayerAction,
indicating that we are are currently deciding on the actions of a particular
player. Because our previous action was START_MOVE the only two subequent
available action types are MOVE or END_PLAYER_TURN. The board state now
includes roll probabilities for movement success.
ActionType.MOVE (id = 22)
{'x': 15, 'y': 10}
{'x': 13, 'y': 11}
{'x': 15, 'y': 11}
{'x': 13, 'y': 12}
{'x': 14, 'y': 12}
{'x': 15, 'y': 12}
ActionType.END_PLAYER_TURN (id = 5)
Current procedure: PlayerAction (index = 8)
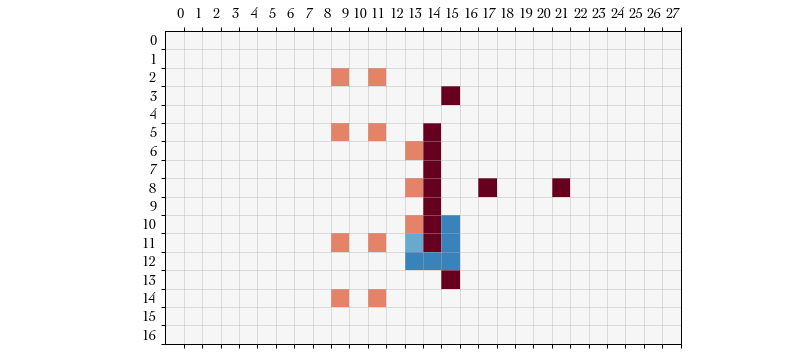
We elect to move the currently selected player to . This isn’t necessarily a good strategy (a block is a better action, here) but I’m just illustrating some of the game states and the corresponding restricted action space.
action = {
'action-type': 22, # MOVE
'x': 13,
'y': 12,
}
observation, reward, is_terminal, _ = environment.step(action)
Action #3: USE_REROLL – The probability of successfully moving our player
to that position was low and one of the defensive linemen tripped up our player.
The game is now prompting us if we would like to try the move action again by
spending a reroll, as implied by the Dodge procedure. If we don’t then our
player is downed.
ActionType.USE_REROLL (id = 6)
ActionType.DONT_USE_REROLL (id = 7)
Current procedure: Dodge (index = 17)
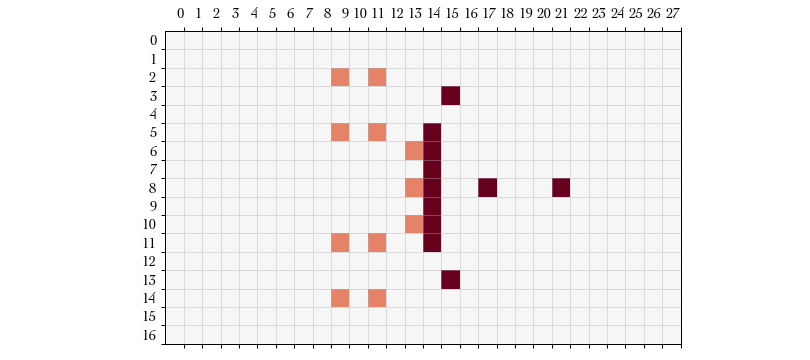
We elect to use one of our rerolls. The reroll action type does not accept
positional input so we can enter whatever we like for x and y.
action = {
'action-type': 6, # USE_REROLL
'x': -1,
'y': -1,
}
observation, reward, is_terminal, _ = environment.step(action)
Action #4 START_BLOCK – It turns out we were unsuccessful in the dodge
reroll. We know this in two ways: first we re-enter the Turn procedure
allowing us a wide possible number of actions with the remaining players on our
team. Second, the board feature space no longer include the player we just moved
in the “standing players” feature, though is still of course in the “own
players” feature. Below, I colored the downed player at in a
lighter shade of red.
ActionType.START_MOVE (id = 27)
{'x': 15, 'y': 3}
{'x': 14, 'y': 5}
{'x': 14, 'y': 6}
{'x': 14, 'y': 7}
{'x': 14, 'y': 8}
{'x': 17, 'y': 8}
{'x': 21, 'y': 8}
{'x': 14, 'y': 9}
{'x': 14, 'y': 10}
{'x': 13, 'y': 12}
{'x': 15, 'y': 13}
ActionType.START_BLOCK (id = 28)
{'x': 14, 'y': 5}
{'x': 14, 'y': 6}
{'x': 14, 'y': 7}
{'x': 14, 'y': 8}
{'x': 14, 'y': 9}
{'x': 14, 'y': 10}
... (snip) ...
ActionType.END_TURN (id = 8)
Current procedure: Turn (index = 7)
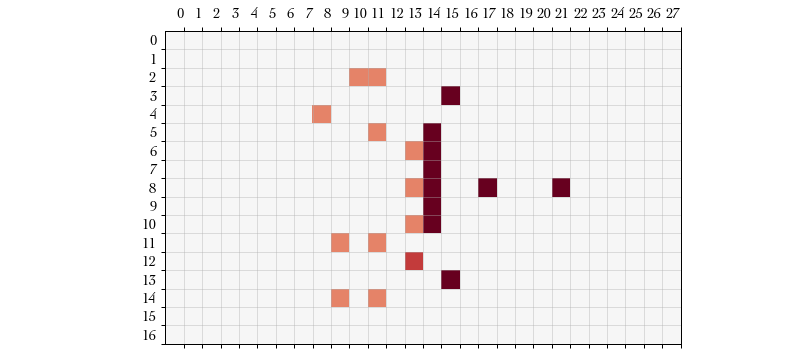
Let’s see how blocking is played out. On this action we will begin a block action with the player at . For brevity I will omit the action definitions for the rest of this example.
Action #5: BLOCK – After selecting START_BLOCK with the player at
we are given a list of possible targets, which in this case is
the single opponent opposite of the blocker. The board’s roll probabilities
feature now shows the probability of success for this block. (Shown in blue in
the plot below.)
ActionType.BLOCK (id = 23)
{'x': 13, 'y': 6}
ActionType.END_PLAYER_TURN (id = 5)
Current procedure: PlayerAction (index = 8)
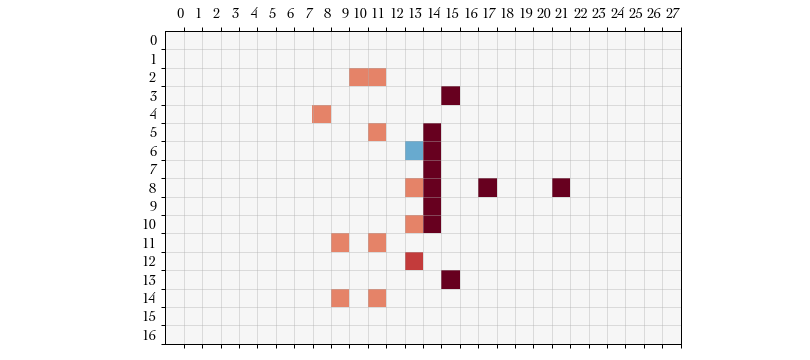
We block our lone opponent in .
Action #7, #8: SELECT_DEFENDER_STUMBLES and PUSH – Blocking in Blood
Bowl involves rolling a number of six-sided dice and choosing a result from one
of the dice. The possible results are (1) attacker down, (2) both down, (3)
pushed, (4) pushed, (5) defender stumbles, and (6) defender down. In our block
attempt we are allowed to roll two dice and choose the result we prefer.
ActionType.USE_REROLL (id = 6)
ActionType.SELECT_PUSH (id = 12)
ActionType.SELECT_DEFENDER_STUMBLES (id = 13)
Current procedure: Block (index = 9)
SELECT_DEFENDER_STUMBLES is a better result because our opponent doesn’t have
the “dodge” ability and therefore will count as a defender down. Immediately
following this action we enter the Push procedure and choose a square into
which we push our opponent. Our blocker pushes his opponent into .
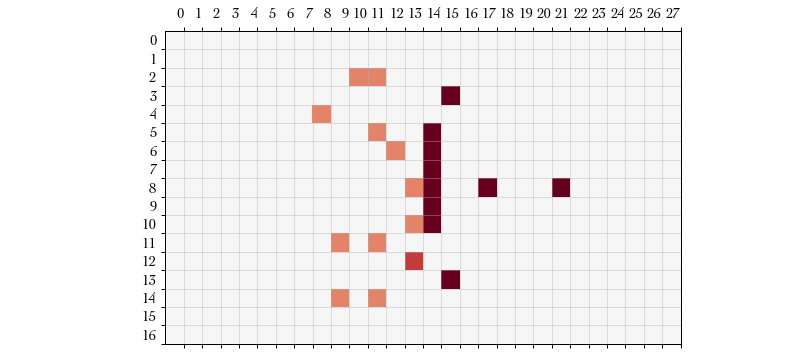
Action #9: FOLLOW_UP – Finally, after every successful push we have the
option to move into the opponent’s previous location. This option is presented
to us as a FOLLOW_UP action with two possible locations: our current location
and the defender’s previous location. We elect to enter the opponent’s square. I
indicate that the defender was downed by using a lighter shade of orange.
Now that the blocking player has completed their actions we are back to the
Turn procedure where we can choose a new player to perform an action.
ActionType.START_MOVE (id = 27)
{'x': 15, 'y': 3}
{'x': 14, 'y': 6}
{'x': 14, 'y': 7}
{'x': 14, 'y': 8}
{'x': 17, 'y': 8}
{'x': 21, 'y': 8}
{'x': 14, 'y': 9}
{'x': 14, 'y': 10}
{'x': 13, 'y': 12}
{'x': 15, 'y': 13}
ActionType.START_BLOCK (id = 28)
{'x': 14, 'y': 7}
{'x': 14, 'y': 8}
{'x': 14, 'y': 9}
{'x': 14, 'y': 10}
... (snip) ...
ActionType.END_TURN (id = 8)
Current procedure: Turn (index = 7)
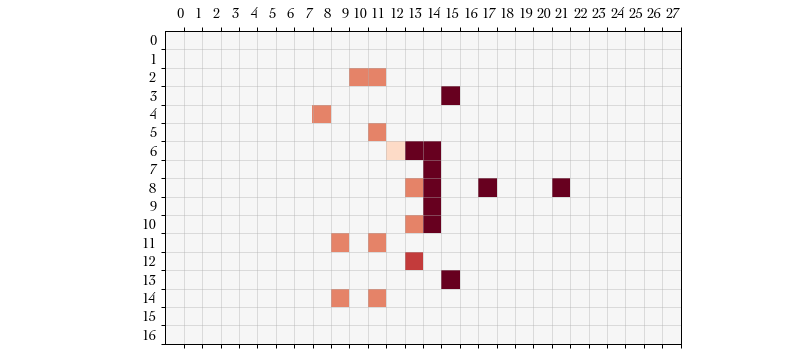
Depending on how you count them, the environment action space can be quite
large. While there are only thirty-seven distinct action types, twenty-two of
them require positional input. Given that the standard pitch
contains four-hundred seventy-six locations is it possible to discretize our
action space all of these actions-position pairs? That is, could our
action-value function consist of, say, more than four-hundred different MOVE
actions, four-hundred different PASS actions, etc.? If we did then there would
be a total of, possible actions.
Is 10487 discrete actions considered large? Let’s compare to DeepMind’s AlphaGo [Silver, 2016] and AlphaStar [Vinyals, 2019] algorithms. Go has board locations and the only in-game action is the placement of a board. The introduction to the AlphaStar paper claims there are possible actions. No number of GPUs or TPUs could possibly output state-action values for this many actions. Instead, the action space is decomposed into approximately 300 action types and 13 action parameters where two of these parameters are the -coordinates of the playing field. See [Vinyals, 2017] (SC2LE) for a full description of the environment and to get a better sense as to how the game is represented.
This idea of action-type/parameter decomposition is also seen in [Hausknecht 2019]. Under this kind of framework, though, we have to re-work the learning algorithms a bit. I’ll dive deeper into some of these things in the next post.
Another key observation is that the one-hot procedure vector is crucial for proper action selection. We are usually limited to a subset of the action space depending on the current procedure. Storing this information as a one-hot is natural for whatever model we choose: suppose a unit at some point of the network is a concatenation of the procedure vector with other data from the game. If this unit is fed into a linear layer then the “one-hottedness” acts like a switch by deactivating some of the weights. We can think of that layer containing several sub-matrices, one for each of the nineteen procedures.
Finally, for testing purposes I am considering filtering out some of the state
in order to speed up testing. The board layers “block”, “dodge”, “sure hands”,
“catch”, and “pass”, while important in the game of Blood Bowl, are very sparse.
As a result, the probability that these skills will be learned is very low. As
for the state, features like own/opp fame, own/opp assistant coaches,
own/opp babes, and own/opp cheerleaders are very high level features that
have relatively small impact on the game.
Unfortunately, due to the complexity of the game and the dependence on position-specific actions I will need to use a post to explore different reinforcement learning algorithms. In my next post I will take a look at models that work well with parametrized actions as well as some improved agent strategies from the three basic strategies discussed in the previous post.