Towards the Abel Map

As much as I just want to jump into implementing the Abel map the more I think about it the more I beleive I need to establish a solid data model before doing so. In another post I’ll describe my thoughts on this matter by discussing divisor and place constructs. For now, I wanted to share some thoughts about computing paths to so-called “singular (discriminant) places” on a Riemann surface.

The two major (abstract) classes at play are

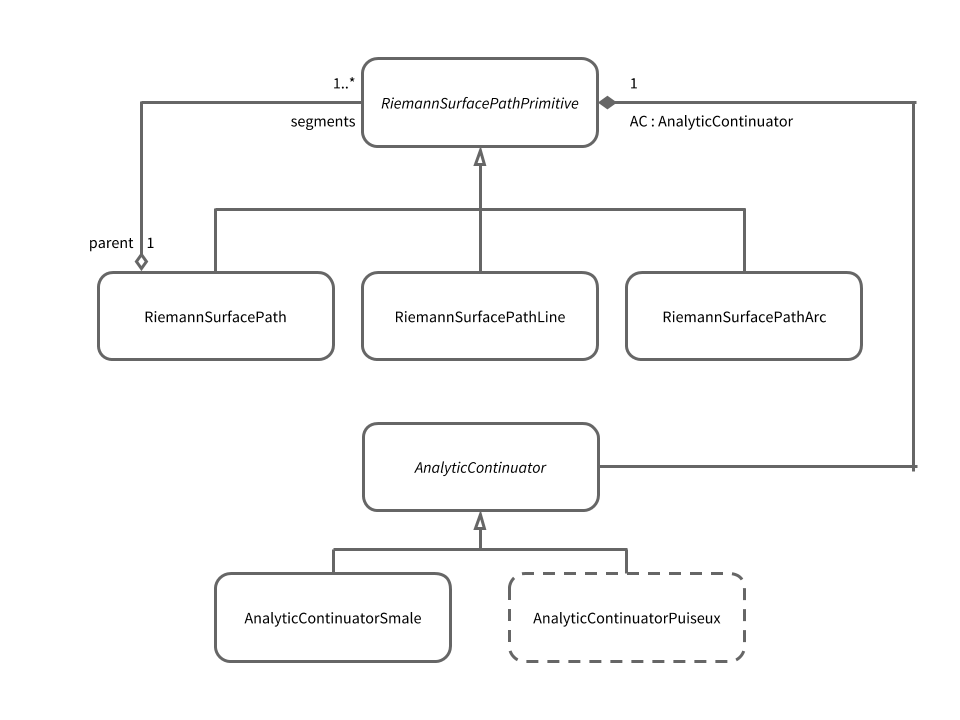
• RiemannSurfacePathPrimitive
• AnalyticContinuator

The RiemannSurfacePath class follows a composite design pattern with RiemannSurfacePathPrimitive as its primitive / base class. A RiemannSurfacePathPrimitve encapsulates the geometry of a Riemann surface path. In particular, the Line and Arc classes define how to traverse a path on the surface where the $x$-part of the path is a line segment or arc, respectively, in the complex plane. (Thoughout abelfunctions we interpret a Riemann surface as the desingularization and compactification of a complex algebraic curve given in some affine coordinate frame.) All paths are made up from these two geometric items.

Each RiemannSurfacePathPrimitive contains an AnalyticContinuator class instance which performs the actual analytic continuation along the path; that is, the analytic continuation of some fibre of $y$-roots, $y\_1, \\ldots, y\_{d}$ where $d$ is the $y$-degree of the curve $C : f(x,y) = 0$ from some $x_i$ in the complex plane to some other $x_{i+1}$. Without the AnalyticContinuator a RiemannSurfacePath wouldn’t know what the $y$-part of the path looks like.

The class diagram for these objects looks like this

Again, every RiemannSurfacePath defers analytic contination of $y$-fibres along $x$-paths to a contianed AnalyticContinuator object. Currently, there is only one kind of analytic continuator implemented which uses Smale’s alpha theory; a verifiable method of using Newton iteration for numerical root finding. This method is used whenever the $x$-part of a Riemann surface path is sufficiently far away from any discriminant points of a curve; that is, points where two of more $y$-roots coalesce into one with multiplicity.

Approaching Branch Points

If, on the other hand, the $x$-part is near or at a discriminant point then we need to use a Puiseux series expansion of the curve in order to accurately capture the local geometry and therefore, “analytically continue” our $y$-fibres. The (crudely drawn) image below describes what is going on.

Suppose at the discriminant / branch point $b$ there are two places lying above it, $P$ and $Q$. That is there are two places on the Riemann surface whose $x$-projection to the underlying curve is equal to $b$. In this particular example it just so-happens that the $y$-projections are equal, as well; an additional challenge that may be present. At any regular point $x=a$ of the curve there are always $n = \text{deg}\_y f$ places lying above it whose $y$-projections are distinct by regularity, shown in the figure above as $P\_1$, $P\_2$, and $P\_3$.

In order to analytically continue to $x=b$ I need to compute the Puiseux series expansions of each fibre element at the point $x=b$ and use these series to keep track of which root is which. (A PuiseuxTSeries object represents a collection of conjugate PuiseuxXSeries. In a sense, a PuiseuxTSeries is synonymous with a place on the corresponding Riemann surface.) There are a number of computational and software design challenges with this concept:

1. How do I efficiently match each PuiseuxXSeries with the corresponding root at $\tilde{x}$?
2. How do I determine how many terms of each PuiseuxXSeries I need to compute in order to accurately perform the matching in 1. above?
3. Which part of the code should perform the matching and term generation? Do I let the PathFactory object determine this? The RiemannSurfacePath? The AnalyticContinuator itself?
4. (Later) What about Puiseux series at infinity?

The answers to these questions depend on some choice of data model for places and divisors on a Riemann surface and this is something that I’m currently designing and implementing.

Related Board Work

Below are some scribblings and notes I made on the arrangement of these classes.

Board #1. Here I have some notes about the relationship between the analytic continuators and Riemann surface paths. I write some thoughts about how the AnalyticContinuator.analytically_continue() function should work. Based on some discussions with Daniel I think there will need to be a close dependency on the path itself in the construction of the continuator. In particular, the starting fibre of the path (I need to initialize paths with an entire fibre of $y$-roots in order for Smale to work) will determine the ordering of the underlying PuiseuxXSeries as well as the number of terms needed in each.

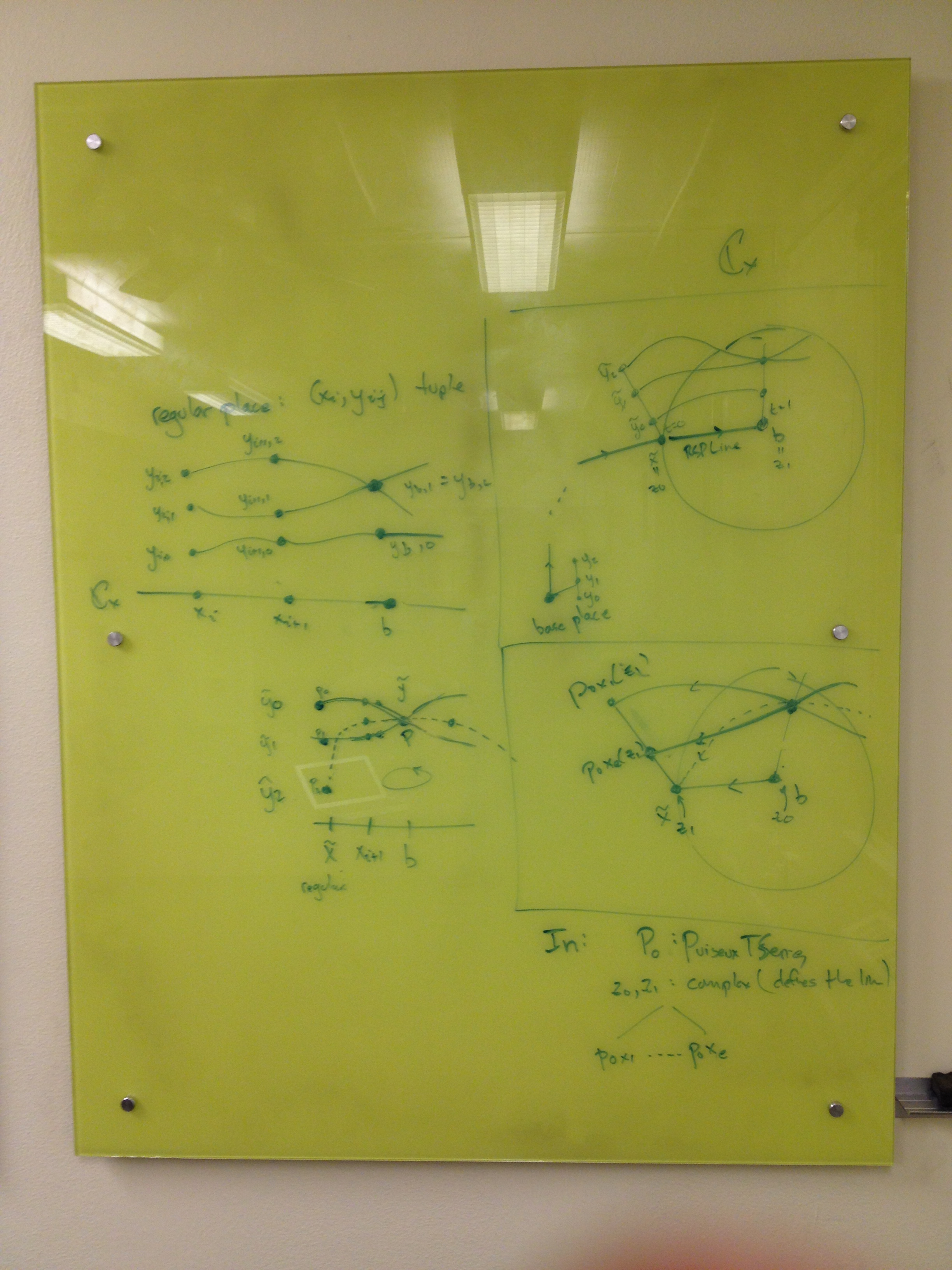
Board #2. Here I scribble some throughts about Puiseux series matching. I identified that there are two cases to consider:

1. the “starting place / fibre” is at the beginning of the path,
2. the starting place is at the end of the path.

The latter case appears when somebody wants to construct a path starting at a place (synonymous with a PuiseuxTSeries) $P$ where the $x$-part of the place is a branch point of the curve.